Grundlagen der Sprache
- Die ersten Befehle in eingeben
- Einen Eindruck vom Umgang mit bekommen
Dieses Kapitel führt in die grundlegende Funktionsweise der Sprache ein. Wie bei jeder Sprache tauchen dabei Begriffe auf, die unbekannt oder ungewohnt sind bzw. in der jeweiligen Sprache eine besondere Bedeutung haben. Lassen Sie sich von Begriffen wie Objekt, Funktion oder Operator nicht abschrecken. Am Ende des Buches werden diese zu ihrem -Standard-Wortschatz zählen und ihre Bedeutung innerhalb von wird verständlich sein.
R als Taschenrechner
funktioniert interaktiv in einem Frage-Anwort Modus. Wenn man z.B. etwas in die Konsole eingibt und die Eingabetaste drückt, wird das Eingegebene ausgewertet. Auf diese Weise kann wie ein Taschenrechner genutzt werden:
1 + 1
[1] 210 - 5
[1] 5Wie im vorangehenden Beispiel deutlich wird, können die grundlegenden arithmetischen Operationen (d.h.+ - * /)genutzt werden. Klammern können in der üblichen Weise verwendet werden und markieren den Vorrang einer Operation vor einer anderen Operation.
3 * (1+1)
[1] 6(2+2)/(1+1)
[1] 2Pro Zeile können ein oder mehrere Befehle in die Konsole eingegeben werden. Wenn mehrere Befehle in einer Zeile stehen, muss das Ende jedes einzelnen Befehls durch ein Semikolon (;) gekennzeichnet werden. Ein Semikolon markiert in jeweils das Ende eines Befehls. Für den letzten Befehl in einer Zeile kann das Semikolon weggelassen werden. Da es üblich ist, nur einen Befehl pro Zeile zu schreiben, findet man selten Semikolons im Code.
1 + 1; 2 + 2; 3 + 3
[1] 6Befehle können sich auch über mehrere Zeilen erstrecken. überprüft jeweils die eingegeben Befehle. Wenn ein Befehl am Ende einer Zeile oder bei einem eingefügten Zeilenumbruch noch nicht abgeschlossen ist, wird das Ende eines Befehls in den nachfolgenden Zeilen suchen. Der Befehl wird erst dann ausgeführt, wenn er vollständig ist. Im nachfolgenden Beispiel erwartet noch eine weitere Ziffer, da die Zeile mit einem Minus-Zeichen endet und der Befehl somit noch nicht vollständig ist. Dass ein Befehl noch nicht abgeschlossen ist zeigt dadurch an, dass es anstatt dem üblichen Größer-Als-Zeichen (>) ein Pluszeichen am Zeilenanfang ausgibt. Lassen Sie sich durch das Pluszeichen nicht verwirren, es dient nur als Hinweis, dass noch ein Teil des Befehls fehlt.
1 - 2 - 3 -
4 - 5
[1] -13Manchmal kommt es vor, dass man Fehler in den Code einbaut, die dazu führen, dass immer weiter auf den Abschluss des Befehls wartet. In diesem Fall kann die Eingabe durch das Drücken der Escape-Taste abgebrochen werden.
Grundlegende Arithmetische Operationen
Wie bereits dargestellt wurde, können in die grundlegenden arithmetischen Operationen, wie sie aus dem Taschenrechner bekannt sind, genutzt werden. Hierbei gilt die übliche Auswertungsreihenfolge von Operatoren (Punkt- vor Strichrechnung). Eine Liste der grundlegenden arithmetischen Operationen findet sich in Tabelle XXX.
| Operator | Beschreibung |
|---|---|
4 + 4 |
Addition |
4 / 4 |
Division |
Geben Sie folgende Beispiele ein und schauen Sie, was passiert.
5^2
[1] 25Kommentare im Code
Die Raute (#) hat in eine besondere Bedeutung. Sie leitet sogenannte Kommentare ein. Alles was in einer Zeile hinter der Raute steht, wird von nicht ausgewertet und dient dazu, den Code zu kommentieren. Kommentare sind sehr wichtig, um die eigenen Analysen auch nach Monaten noch nachvollziehen zu können oder dies anderen zu ermöglichen. An Kommentaren sollten Sie nicht sparen! Guter Code enthält stets ausreichend Kommentare, um Dritten den Code verständlich zu machen.
1 + 1 # Hier gehört die Erklärung der Analyse hin
[1] 2Schauen Sie sich noch einmal den Code aus dem Beispiel zum Schnelleinstieg von Seite an. Dort sehen Sie, wie in jeder Zeile Kommentare stehen, die beschreiben, was gerechnet wird.
Außer dafür, Erklärungen in den Code zu schreiben, wird das Kommentarzeichen häufig genutzt, Code auszukommentieren. Denn eine Raute führt dazu, dass alles hinter der Raute als Kommentar interpretiert und nicht ausgeführt wird. Somit bewirkt eine Raute vorm -Code, dass dieser nicht ausgeführt wird. Dies kann nützlich sein, wenn Teile einer Analyse zeitweise nicht mehr ausgeführt werden sollen. Nachfolgend wird 1 + 1 gerechnet, 2 + 2 jedoch nicht, da es als Kommentar gekennzeichnet ist.
1 + 1 # eins plus eins
[1] 2# 2 + 2 # zwei plus zweiDarstellung von Zahlen
Dezimaltrennzeichen
In Deutschland ist es üblich, das Komma als Dezimaltrennzeichen zu verwenden. In nahezu allen Computer-Sprachen und großen Teilen der Welt (Nordamerika, Australien, in Teilen Asiens und Europas) ist dies jedoch der Punkt. Auch nutzt den Punkt als Dezimaltrenner. Kommata haben eine andere Funktion, die wir erst später kennenlernen werden. Weiterhin ist es im englischsprachigen Raum üblich, die Null vor dem Punkt wegzulassen. Dies ist auch bei möglich.
1.1 # Der Punkt ist der Dezimaltrenner, nicht das Komma
[1] 1.1.1 # Dasselbe wie 0.1
[1] 0.1Wissenschaftliche Notation
Mitunter werden sich in dem Output von folgende Ausdrücke finden lassen.
8.164e+01
1.613e-04Hierbei handelt es sich um gewöhnliche Zahlen, die in der wissenschaftlichen Notation (d.h. in Exponentialdarstellung) dargestellt sind. Dies ist in vielen Computerprogrammen der Fall und bedarf der Gewöhnung. Das e in dem Ausdruck steht für 10 hoch. Die erste Zahl ist somit 8. 164 ⋅ 101, d.h. 81. 64. Die zweite Zahl ist 1. 613 ⋅ 10 − 4, d.h. 0. 0001613. Besonders bei sehr kleinen Werten wird diese Notation häufig verwendet, um nicht alle Nullen ausschreiben zu müssen. Uns wird diese Art der Ausgabe später z.B. bei den Ergebnissen einer Regressionsrechnung begegnen.
Missing Values
In existiert das vordefinierte Symbol NA, das für einen fehlenden Wert (missing value) steht. Die Buchstaben NA sind ein Akronym für die Worte not available. Der Ausdruck NA kann wie z.B. eine 1 in die Konsole eingegeben und für Befehle genutzt werden.
NA
[1] NAAuch kann NA zum Beispiel im Rahmen einer Addition genutzt werden.
1 + NA
[1] NADa nicht weiß, um welchen Wert es sich bei dem NA handelt ist auch das Ergebnis nicht bekannt und somit ebenfalls NA. Wenn z.B. der Mittelwert mit der Funktion mean berechnet wird und eine der eingegebenen Zahlen NA ist, so ist das gesamte Ergebnis, analog zur oben stehenden Addition zweier Zahlen, NA. Wir werden den Umgang mit missing values an den entsprechenden Stellen behandeln. Zunächst ist nur wichtig, dass NA die -interne Definition für missing values ist.
Rechenergebnisse speichern
Rechnungen in durchzuführen und sich das Ergebnis anzeigen zu lassen ist hilfreich. Um das erhaltene Ergebnis jedoch für weitere Rechenschritte nutzen zu können, muss es gespeichert werden. In geschieht dies mittels des sogenannten Zuweisungsoperators. Dieser hat die Aufgabe, das Ergebnis eines Ausdrucks (z.B. 1 + 1) einem Objekt zuzuweisen. Der Zuweisungsoperator besteht aus zwei Zeichen: einem Kleiner-als-Zeichen und einen Minus (<-). Um eine Rechnung zu speichern, wird auf der linken Seite vom Zuweisungsoperator ein Objekt benannt, in welches das Ergebnis gespeichert werden soll (z.B a). Rechts von dem Zuweisungsoperator steht der Ausdruck dessen Ergebnis gespeichert werden soll (z.B. 1 + 1).1
Folgender Code speichert z.B. das Ergebnis der Rechnung 1 + 1 in dem Objekt a.
a <- 1 + 1Der Code erzeut das Objekt a und speichert in diesem das Ergebnis des Ausdrucks, der auf der rechten Seite vom Zuweisungsoperatoir steht (hier 2). Um das Ergebnis, d.h. den Inhalt von a, anzuzeigen, muss der Name des Objektes in die Konsole eingegeben werden.
a
[1] 2Wann immer Sie in den Namen eines Objektes in die Konsole eingeben und die Enter-Taste drücken wird sein Inhalte ausgegeben. Was genau ein Objekt ist wird im Folgenden näher erläutert.
Objekte
Eben haben wir das Ergebnis einer Rechnung in einem sogenannten Objekt gespeichert. In ist es möglich, verschiedenste Ergebnisse in Objekten zu speichern. Dies können Zahlen, Buchstabenfolgen, Koeffizienten einer Regression, Ladungen einer Faktorenanalyse oder auch ein Dutzend verschiedene Regressions-Analysen sein. Man kann sich ein Objekt am besten als einen Container oder Behälter vorstellen, der alles Mögliche enthalten kann. Die Speicherung des Ergebnisses eines Ausdrucks in einem Objekt ermöglicht es, dieses in nachfolgenden Rechnungen zu verwenden. Da in dem Objekt a zurzeit eine Zahl enthalten ist, kann das Objekt auch wie eine Zahl verwendet werden, d.h. man kann es addieren, multiplizieren, subtrahieren etc. Das Objekt kann somit wie eine mathematische Variable verwendet und in einen weiteren Ausdruck eingebaut werden. Denn der Name des Objekts ist nur ein symbolischer Platzhalter für den in ihm enthaltenen Wert. In unserem Fall könnte das Objekt a, das zurzeit den Wert 2 enthält, wie folgt genutzt werden.
3 * a
[1] 6Grundsätzlich kann der Inhalt eines Objektes verändert werden, indem eine erneute Zuweisung an das Objekt erfolgt. Nachfolgend wird dem Objekt a der neue Wert 10 zugewiesen. Der vorherige Inhalte 2 ist dann überschrieben und nicht mehr verfügbar.
a <- 10Bisher haben wir nur das Objekt a erzeugt. Grundsätzlich kann ein neues Objekt dadurch erzeugt werden, dass es links vom Zuweisungsoperator benannt wird. Im Folgenden wird im Objekt b die Zahl 10 gespeichert. Danach werden die Objekte a und b (beides Zahlen) multipliziert und in dem Objekt d gespeichert.
b <- 10
d <- a * b
d
[1] 100Bisher haben wir nur Zahlen in Objekten gespeichert. Nun soll in dem Objekt a die Zeichenkette "abc" gespeichert werden. Einzelne Zeichen und Zeichenketten werden in stets in einfache oder doppelte Anführungszeichen gesetzt ('abc' oder "abc"). Anders als in vielen anderen Programmiersprachen darf in jedes Objekt nacheinander verschiedenartige Typen von Werte enthalten (z.B. Zahlen, Zeichenketten etc.). Dies muss vorher nicht explizit definiert werden. Es reicht, dem Objekt einfach einen neuen Wert zuzuweisen. Wenn a also vorher eine Zahl enthielt, enthält es durch Zuweisung der Zeichenkette "abc" danach eine Zeichenkette.
a <- "abc"
a
[1] "abc"Der Typ des Objekts a hat sich nun von Zahl auf Zeichenkette geändert. Einerseits ist diese Art der Zuweisung einfach in der Handhabung. Andererseits muss man aufpassen, welche Art von Daten (Zahl, Zeichenkette etc.) einem Objekt zugewiesen wurden. So ist z.B. die Muliplikation einer Zeichenkette mit einer Zahl nicht definiert und erzeugt einen Fehler.
a * 10 # verursacht einen Fehler
Error in a * 10 : non-numeric argument to binary operatorBenennung von Objekten
Bisher haben wir Objekte mit den Namen a, b und d erzeugt. Grundsätzlich ist es möglich, Objekte nahezu beliebig zu benennen. Kürzel wie a sind jedoch oft nicht aussagekräftig und dienen nicht dem Verständnis des Codes. Sinnvoll ist es, sprechende Namen zu nutzen. Bei der Benennung sind lediglich einige wenige Regeln zu beachten:
Objektnamen können aus Buchstaben, Zahlen, Punkten und Unterstrichen bestehen:
object1 <- 10object.1 <- "hallo"object_1 <- 10Objektnamen dürfen keine Operatoren enthalten (
+,-,*,/etc.).object-1 # nicht möglichObjektnamen dürfen nicht mit einer Zahl oder von einem Punkt gefolgt von einer Zahl beginnen.
1object # nicht möglich.1object # nicht möglichGroß- und Kleinschreibung wird unterschieden.
aundAist nicht dasselbe. Dies kann systematisch genutzt werden, um Objektnamen durch gezielte Großbuchstaben leserlicher zu gestalten:myobject <- 10myObject <- 10
Eine umfassende Übersicht über den Stil, in dem man in Objekte und Funktionen benennt und Code strukturiert, findet sich unter http://google-styleguide.googlecode.com/svn/trunk/google-r-style.html. Hier finden sich diverse Code-Elemente, die zu diesem Zeitpunkt noch nicht eingeführt wurden. Es lohnt sich jedoch, sich schon einmal einen Eindruck zu verschaffen.
Logische Operationen
Bisher haben wir die grundlegenden arithmetischen Operationen kennengelernt. In diesem Kapitel werden logische Operationen eingeführt. Solche Operationen sind notwendig, um etwas zu überprüfen. Zum Beispiel ob der Datensatz Personen mit einem IQ größer als 120 enthält. Logische Operationen können dazu dienen, sehr komplexe logische Fragen zu konstruieren: Gibt es Personen, die einen IQ größer als 120 haben, männlich sind sowie geschiedene Eltern haben?
Um in logische Vergleiche anzustellen, stehen eine Reihe von Operatoren zur Verfügung. Ein einfacher Vergleich ist der Größer-als-Vergleich, z.B. ist 2 größer als 1?
2 > 1
[1] TRUEgibt hier den Wert TRUE zurück. Neben größer als können weitere logische Abfragen durchgeführt werden.
| Operator | Beschreibung | Ergebnis |
|---|---|---|
1 == 2 |
ist 1 gleich 2? |
FALSE |
1 != 2 |
ist 1 ungleich 2? |
TRUE |
1 > 2 |
ist 1 größer 2? |
FALSE |
1 >= 2 |
ist 1 größer gleich 2? |
FALSE |
1 < 2 |
ist 1 kleiner 2? |
TRUE |
1 <= 2 |
ist 1 kleiner gleich 2? |
TRUE |
Die in der Tabelle beschriebenen Abfragen geben die Werte TRUE oder FALSE zurück. Dies sind die in definierten logischen Konstanten, die für wahr und falsch stehen. Wie aus der Oberstufenmathematik bekannt, kann man Wahr- und Falschaussagen mit dem logischen UND und ODER verknüpfen. So kann man fragen: Ist A und B wahr? Dies ist nur dann der Fall, wenn beide Werte wahr sind. Würde ich Sie zum Beispiel bitten, Ihre Hand zu heben, wenn Sie älter als 20 Jahre sind und aus dem Norden von Deutschland kommen, würden sie dies nur dann tun, wenn beide Eigenschaften auf Sie zutreffen. Es handelt sich hierbei um ein logische UND-Verknüpfung. Das logische ODER funktioniert analog: Ist A oder B wahr? Dies ist dann der Fall, wenn mindestens einer der Werte wahr ist. Würde ich Sie bitten, Ihre Hand zu heben, wenn sie über 20 Jahre alt sind oder aus dem Norden kommen, würden Sie dies tun, auch nur eine der Eigenschaften auf Sie zutrifft. In stehen für die beiden Verknüpfugstypen die logischen Operatoren & (logisches UND) und | (logisches ODER) zur Verfügung. Die Verknüpfungen, die möglich sind, sind in Tabelle Logische Verknüpfungen dargestellt.
Tabelle: Logische Verknüpfungen
| Werte | Beschreibung | Ergebnis |
|---|---|---|
TRUE | TRUE |
sind beide Werte wahr? | TRUE |
TRUE | FALSE |
sind beide Werte wahr? | FALSE |
FALSE | TRUE |
sind beide Werte wahr? | FALSE |
FALSE | FALSE |
sind beide Werte wahr? | FALSE |
TRUE | TRUE |
ist mindestens einer der Werte wahr? | TRUE |
TRUE | FALSE |
ist mindestens einer der Werte wahr? | TRUE |
FALSE | TRUE |
ist mindestens einer der Werte wahr? | TRUE |
FALSE | FALSE |
ist mindestens einer der Werte wahr? | FALSE |
Eingangs haben wir gesagt, dass logische Operationen dabei helfen, komplexe Fragen zu konstruieren. Wie können wir mit dem bisherigen Wissen eine logische Frage konstruieren? Nehmen wir an, wir haben eine Person mit einem IQ von 120 und einem Extraversionswert von 90. Wir wollen nun z.B. wissen, ob die Person beim IQ und beim Extraversionswert über dem Mittel von 100 liegt.
iq <- 120 # IQ sei 100
extra <- 90 # Extraversion sei 90
iq > 100 # ist der IQ größer 100?
[1] TRUE
extra > 100 # ist Extraversion größer 100?
[1] FALSEDiese beiden logischen Abfragen können zu einer einzigen logischen Abfrage gemäß Tabelle [tab:logischeverknuepfungen] kombiniert werden. Die Klammern sind hierbei nicht zwingend notwendig. Sie dienen in dem Beispiel nur zur Verdeutlichung.
(iq > 100) & (extra > 100) # sind der IQ und die Extraversion größer 100?
[1] FALSEDa die Person nicht bei beiden Werten über dem Durchschnitt 100 liegt wird der Wert FALSE zurückgegeben (denn TRUE & FALSE ergibt FALSE).
Neben den Konstanten TRUE und FALSE stehen in die Kurzformen T und F zur Verfügung, die alternativ verwendet werden können. Der Übersicht halber ist es jedoch ratsam, TRUE und FALSE auszuschreiben.
T & T
[1] TRUEF | T
[1] TRUEEine weiterer wichtiger logischer Operator ist die logische Negation. Ein logischer Ausdruck (TRUE oder FALSE) kann durch das Voranstellen eines Ausrufezeichens in sein Gegenteil verwandelt werden. Die Negation von TRUE ist FALSE und umgekehrt.
! TRUE
[1] FALSE
! FALSE
[1] TRUE
! TRUE | FALSE
[1] FALSEWir werden später sehen, dass der Operator häufig verwendet wird, um zu testen, ob eine bestimmte logische Aussage (z.B. iq > 100) zutrifft und wenn dies nicht der Fall ist, entsprechend zu handeln.
Funktionen
Argumente und ihre Reihenfolge
Bisher haben wir verschiedene Operatoren (+, -, &, | etc.) kennengelernt, die z.B. eine Addition, Subtraktion etc. durchführen. Neben diesen grundlegenden Operatoren verfügt über einen immensen Umfang an weiteren Funktionen, die jeweils spezielle Aufgaben übernehmen. Das Wort Funktion (lat. functio) heißt übersetzt soviel wie Tätigkeit oder Verrichtung. Eine Funktion ist also ein Objekt, das eine Tätigkeit durchführt. Eine solche Tätigkeit könnten z.B. die Berechnung einer Summe, einer Varianz, einer Regression, einer Faktorenanalyse usw. sein. Nahezu alles, was in geschieht, wird mittels einer Funktion vollzogen.
Funktionen sind in stets daran zu erkennen, dass sie ein bestimmtes Format haben. Es steht zuerst der Name der Funktion. Danach folgt eine öffnende runde Klammer ((), dann ggf. diverse weitere Ausdrücke und zum Schluss eine schließende runde Klammer ()). Wann immer einem in runde Klammern begegnen, so wird es sich um eine Funktion handeln.2
funktionsname(argument.1, argument.2)Innerhalb der runden Klammern kann eine Funktion sog. Argumente entgegennehmen. Diese geben der Funktion genaue Anweisungen darüber, wie sie ihre Verrichtung ausführen soll.
Um ein besseres Verständnis von dem Begriff Funktion und Argument zu erlangen, kann man sich z.B. einen Audio-Verstärker vorstellen. Dieser erfüllt die Funktion (Verrichtung) Sound zu erzeugen. Der Verstärker erhält hierzu ein Eingangssignal (z.B. von einem MP3-Player), das er verstärkt. Darüber hinaus verfügt er i.d.R. über diverse Einstellungsknöpfe, um z.B., die Lautstärke oder die Klangfarbe einzustellen. Das Eingangssignal und die Einstellungen der Knöpfe sind übertragen auf den Begriff Funktion die Argumente. Argumente sind all das, was als Information in eine Funktion hineingegeben wird. Man sieht an diesem Beispiel, dass die Argumente somit zum einen den Input (Eingangssignal) enthalten als auch Möglichkeiten zur Feineinstellung (Lautstärke, Klangfarbe) bieten. Es hängt nun von den einzelnen Argumenten ab, wie genau die Verrichtung “Verstärkung” ausgeführt wird (welches Lied, laut oder leise, viel Bass oder viele Höhen). Dies ist in ebenso: Die Argumente regeln, was genau eine Funktion tut.
Schauen wir uns zunächst die Funktion rnorm an. Der Name der Funktion rnorm steht für random normal. Die Aufgabe der Funktion ist es, zufällige, normalverteilte Werte zu erzeugen. Innerhalb der Klammer erwartet die Funktion zumindest ein Argument das angibt, wie viele zufällige Werte erzeugt werden sollen. Die folgende Zeile Code erzeugt vier zufällige Werte.
rnorm(4)
[1] -0.6157 1.5047 0.1924 0.4279Jedes Argument einer Funktion hat einen Namen, das mit in die Klammer eingefügt werden kann. Hinter dem Namen eines Arguments steht ein Gleichheitszeichen, dahinter folgt der Wert für das Argument. Wir hätten im vorherigen Beispiel den Namen des Arguments hinzufügen können. Das Argument heißt n.
rnorm(n=4)
[1] 0.17722 -0.06424 -1.68741 0.96417Wie viele und welche Argumente eine Funktion entgegennimmt ist von Funktion zu Funktion verschieden. Die Funktion rnorm kennt neben dem Argument n noch die Argumente mean und sd. Dabei bezeichnet mean das Zentrum und sd die Standardabweichung der Normalverteilung, aus der die zufälligen Werte entnommen werden. Wenn eine Funktion mehrere Argumente hat werden diese stets durch Kommata voneinander getrennt. Nachfolgender Befehl erzeugt vier zufällige Wert, die aus einer Normalverteilung mit dem Mittelwert 100 und einer Standardabweichung von 15 entstammen.
rnorm(n=4, mean=100, sd=15)
[1] 108.24 76.73 97.84 50.32Welche Funktion welche Argumente hat und wie man dies herausfindet, wird im nächsten Kapitel ausführlich behandelt. Zunächst sollen jedoch am Beispiel von rnorm einige weitere grundlegende Eigeschaften von Funktionen und die Art und Weise wie man eine Funktion aufruft dargestellt werden.
Im vorletzten Code-Beispiel wurde die Funktion rnorm aufgerufen, ohne die Argumente mean oder sd anzugeben. Trotzdem hat die Funktion Werte ausgegeben. Der Grund dafür ist, dass beim Aufruf einer Funktion nicht alle, sondern nur jene Argumente angegeben werden müssen, für die keine Voreinstellung vorhanden sind. Manche Funktionen brauchen sogar gar keine Argumente, so dass die runden Klammern dann komplett leer bleiben können.
Im Falle von rnorm existieren für die Argumente mean und sd Voreinstellungen, so dass sie beim Aufruf der Funktion ausgelassen werden können. Die Argumente sind wie folgt voreingestellt: mean=0 und sd=1.3 Wird für ein Argument im Funktionsaufruf kein Wert angegeben, so wird die Voreinstellung verwendet. Für rnorm bedeutet dies, dass wenn mean und sd nicht angegeben werden, die Werte 0 und 1 verwendet werden. In diesem Fall werden dann zufällige Werte aus einer Standardnormalverteilung (Mitte Null und Standardabweichung Eins) gezogen.
Rekapitulieren wir kurz: Wir haben bisher gesehen, dass eine Funktion über Argumente verfügt, denen im Funktionsaufruf ein Wert übergeben werden kann. Bei der Funktion rnorm sind es die drei Argumente n, mean und sd von denen zwei Voreinstellungen besitzen und wahlweise angeben werden können.
Reihenfolge von Argumenten
In ist es möglich, die Argumente in beliebiger Reihenfolge anzugeben. Alternativ zum letzten Befehl rnorm(n=4, mean=100, sd=15) hätte man auch Folgendes schreiben können.
rnorm(sd=15, n=4, mean=100)
[1] 134.1 110.1 117.4 102.6Die beiden Befehle sind inhaltich identisch. Beachten Sie jedoch bitte, dass die erzeugten Werte bei jedem Aufruf der Funktion verschiedenen sind, da es sich stest um zufällig erzeugte Werte handelt.
Argumentenamen abkürzen oder weglassen
Bisher wurden die Argumente einer Funktion stets mit dem vollen Namen benannt (z.B. mean). Es ist in erlaubt, die Argumentenamen abzukürzen, indem nur der erste oder die ersten Buchstaben des Namens ausgeschrieben werden (z.B. me für mean) oder den Namen ganz wegzulassen.
Betrachten wir zunächst den Fall der abgekürzten Argumentenamen. versucht abgekürzte Namen stets den vollen Namen der Argumente zuzuordnen. Würden wir z.B. nur m anstelle von mean schreiben, würde das m automatisch als mean deuten. Dies funktioniert jedoch nur dann, wenn die gewählte Abkürzung eindeutig ist und nicht zwei Argumente mit einem m anfangen. Sonst könnte nicht unterscheiden, welches der beiden Argument mit der Abkürzung m gemeint ist und würde einen Fehler erzeugen. Der nachfolgende Code ist identisch mit dem vorherigen, nur das die Namen der Argumente abgekürzt sind.
rnorm(n=4, m=100, s=15)
[1] 116.37 96.82 82.85 85.60Neben der Nutzung von Abkürzungen ist es möglich als auch üblich, die Namen der Argumente ganz wegzulassen.4 Denn für jede Funktion ist eine Standardreihenfolge der Argumente definiert. Bei rnorm ist es: n, mean, sd. Wenn die Namen der Argumente weggelassen werden, nimmt an, dass die Argumente genau in dieser Reihenfolge eingegeben werden. Der folgende Code entspricht somit genau dem vorherigen.
rnorm(4, 100, 15)
[1] 80.04 116.28 99.02 97.33Es ist wichtig zu beachten, dass die Reihenfolge der Argumente nur dann variiert werden kann, wenn die Namen der Argumente benutzt werden. Wenn die Namen weggelassen werden, muss die vorgegebene Standardreihenfolge der Argumente eingehalten werden! Eine letzte Variante Argumente anzugeben ist, nur einige Argumente mit Namen anzugeben und andere in der richtigen Standardreihenfolge anzugeben. Im Folgenden wird das Argument n nicht namentlich benannt, da es sich um das erste in der Standardreihenfolge handelt. sd und mean sind benannt. Dies ist wichtig, da die Reihenfolge sd, mean nicht der definierten Standardreihenfolge entspricht.
rnorm(4, sd=15, m=100)
[1] 112.5 117.5 112.6 101.5Häufige Fehler
Abschließend sei noch auf einen sehr häufig gemachten Fehler hingewiesen: die Kommata zwischen den Argumenten zu vergessen. Dies hat zur Folge, dass einen Fehler ausgibt.
rnorm(n=4 mean=100, sd=15) # verursacht einen Fehler
Error: unexpected symbol in "rnorm(n=4 mean"Überprüfen Sie beim Auftreten eines Fehler deshalb stets als erstes, ob die Syntax stimmt: Stehen alle Kommata am richtigen Ort? Wurde jede geöffnete Klammer auch wieder geschlossen? 90 % der gemachten Fehler sind Syntaxfehler.
Zurückgegebene Objekte einer Funktion
In gibt jede Funktion immer ein Objekt (z.B. eine Zahl, eine Zeichenkette, einen logischen Wert etc.) zurück. Hiervon gibt es in keine Ausnahme. Im letzten Beispiel hat die Funktion rnorm zufällige Werte zurückgegeben. Zwar mag es sein, dass eine Funktion ein Objekt nicht sichtbar zurückgibt, wie z.B. die Funktion hist, die ein Histogramm erzeugt. Dennoch gibt auch hist ein Objekt zurück, das dann sichtbar wird, wenn man es in ein Objekt speichert und dieses in der Konsole ausgeben lässt.
a <- rnorm(100)
hist(a)
h <- hist(a)
h
$breaks
[1] -3.0 -2.5 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 1.5 2.0 2.5 3.0
$counts
[1] 1 4 6 10 9 20 25 13 6 4 1 1Es ist an dieser Stelle nicht möglich und auch nicht von Bedeutung, diesen Output zu verstehen. Es ist nur wichtig im Hinterkopf zu behalten, dass jede Funktionen stets etwas zurückgibt.
Es kann weiterhin der Fall sein, dass eine Funktion ein sogenanntes NULL Objekt zurückgibt. Dies bedeutet, dass die Funktion eigentlich nichts zurückgibt. Dass sie im Grunde nichts zurückgibt, zeigt sie an, indem Sie ein Objekt ohne Inhalt, ein sog. NULL-Objekt zurückgibt. Trotzdem gibt ein Funktion immer etwas, und sei es ein NULL-Objekt, zurück.
plot(1:10)
p <- plot(1:10)
p
NULLDatensätze in
In sind bereits mit der Installation diverse Beispieldatensätze verfügbar. Weitere Datensätze sind in vielen der zusätzlich installierten Pakete enthalten. Die mitgelieferten Datensätze können gut zum Ausprobieren genutzt werden. So müssen nicht erst extra Daten einlesen werden, um Funktionen auszuprobieren.
Die Funktion data listet alle Datensätze aus den Paketen auf, die zurzeit geladen sind (Abbildung [fig:rdatasets]). Datensätze aus Paketen, die nicht geladen sind, werden nicht mit aufgeführt.5
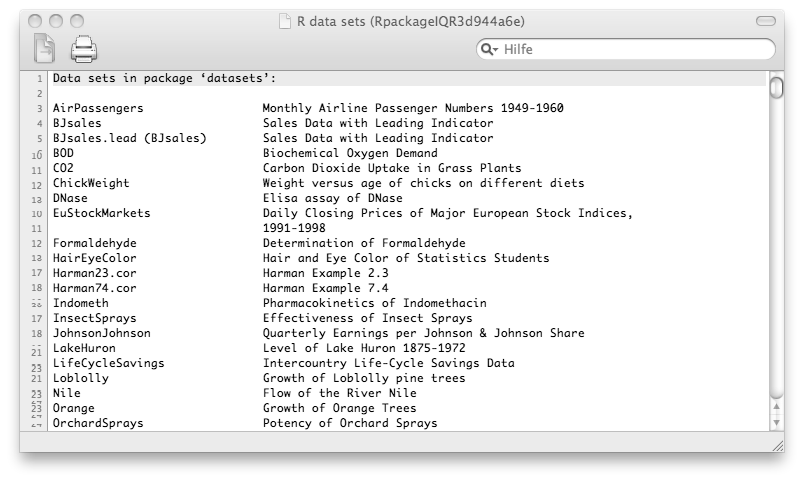
Datensätze in R
Um einen Datensatz aus einem Paket zu nutzen, muss das Paket vorher geladen werden. Danach sind zwei Varianten möglich. Manche Pakete holen ihre Datensätze beim Laden des Pakets automatisch in den Speicher. So zum Beispiel das Paket ggplot2. Nach dem Laden von ggplot2 ist der in dem Paket enthaltene Datensatz economics direkt verfügbar, indem der Name des Datensatzes economics in die Konsole eingegeben wird.
library(ggplot2)
economics
date pce pop psavert uempmed unemploy
1 1967-06-30 507.8 198712 9.8 4.5 2944
2 1967-07-31 510.9 198911 9.8 4.7 2945
3 1967-08-31 516.7 199113 9.0 4.6 2958Bei anderen Paketen müssen die Datensätze zusätzlich in den Speicher geladen werden müssen, bevor sie verfügbar sind. So z.B. bei den Datensätzen aus dem Paket AER. Dies geschieht ebenfalls mittels der Funktion data. Der Name des zu ladenden Datensatzes wird als Argument angegeben, hier der Datensatz Affairs. Der Datensatz ist erst nach dem Laden verfügbar.
library(AER)
Affairs
Error in try(Affairs) : object 'Affairs' not founddata(Affairs)
Affairs
affairs gender age yearsmarried children religiousness education
4 0 male 37 10 no 3 18
5 0 female 27 4 no 4 14
11 0 female 32 15 yes 1 12
occupation rating
4 7 4
5 6 4
11 1 4In der Standardinstallation von , die das Paket datsets enthält, sind bereits ca. 100 Datensätze enthalten (siehe data()). Diese müssen nicht noch extra geladen werden, bevor sie genutzt werden können. Alle Datensätze in verfügen über eine Dokumentation, die beschreibt, welche Bedeutung die Variablen haben. Wie auf diese zugegriffen wird ist im folgenden Kapitel beschrieben.
Es ist auch möglich, den Zuweisungsoperator mit dem Pfeil nach rechts zu verwenden. Dann steht links der Befehl und rechts der Name des Objekts (z.B.
1 + 1 -> a). Dies ist jedoch nicht üblich und sollte aus Gründen der Lesbarkeit nicht gemacht werden. Alternativ kann für eine Zuweisung auch das Gleichheitszeichen genutzt werden (a = 1 + 1). In ist es jedoch üblich, ausschließlich den<-Operator zu benutzen. Auch hier werde ich dieser Konvention folgen, da das Gleichheitszeichen für einen anderen Verwendungszusammenhang vorbehalten bleiben soll, der in Kapitel [sec:funktionen] eingeführt wird.↩Es sei angemerkt, dass nicht alle Funktionsaufrufe über runde Klammern erfolgen. Auch das Plus-Zeichen ist eine Funktion. Zum jetzigen Zeitpunkt ist es jedoch ausreichend, alle Befehle, die eine runde Klammern nutzen, als Funktionen zu identifizieren.↩
Wie man diese herausfindet wird im folgenden Kapitel behandelt. Sie können jedoch dem Vorgreifen und den Befehl
args(rnorm)schon einmal in die Konsole eingeben und den Output inspizieren.↩Wir haben dies im ersten Beispiel mit dem Befehl
rnorm(4)bereits getan.↩Um sich alle Datensätze, die verfügbar sind, d.h. auch jene aus Paketen, die nicht geladen sind, anzeigen zu lassen, kann ebenfalls die Funktion
datagenutzt werden. hierzu dient folgender Befehl:data(package = .packages(all.available = TRUE)). Dieser Befehl ist recht kompliziert und zu diesen Zeitpunkt noch nicht komplett nachvollziehbar. Er ist jedoch manchmal nützlich.↩